穷举搜索实验

实验三 穷举的魅力

一、数据结构简介

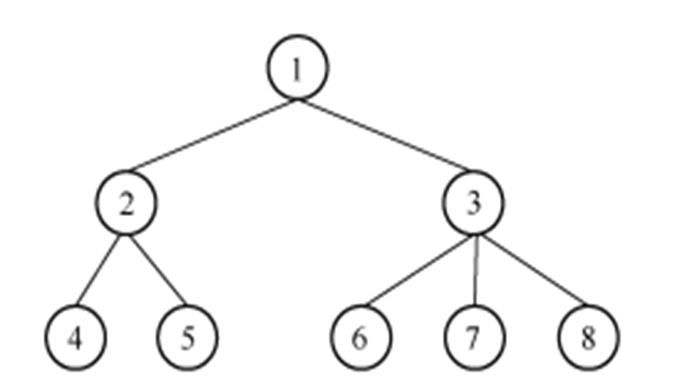
  1. 树

    ​ 树有多个节点，用以存储元素。某些节点之间存在一定的关系，可用连线表示。

    image-20241210091024345

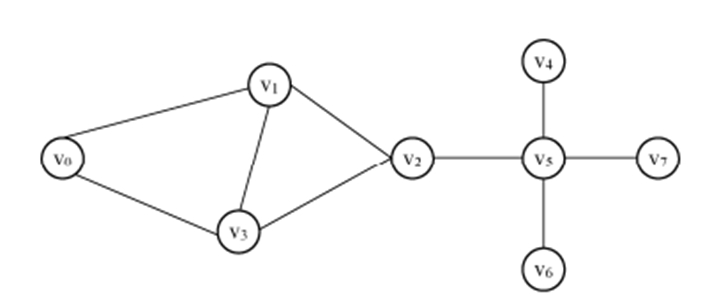
  2. 图

    ​ 图包括有向图和无向图，在此涉及的是无向连通图，在无向图中，顶点之间的边是没有方向的。

    image-20241210091120844

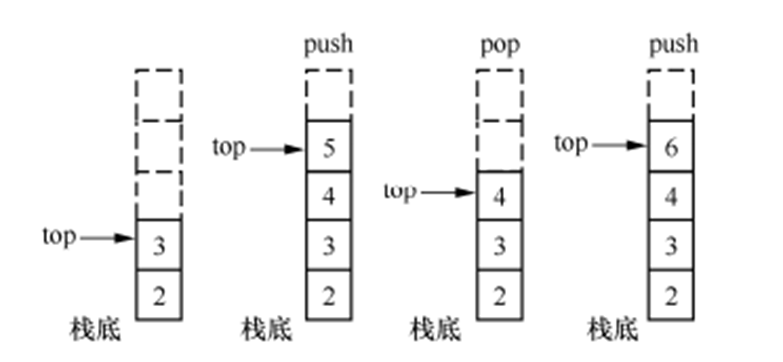
  3. 栈

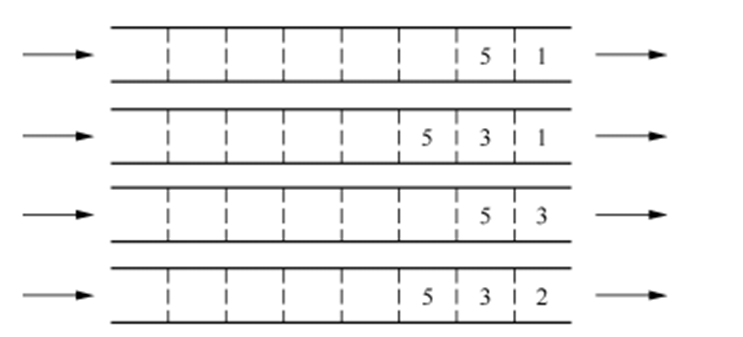
       栈的特点是插入和删除操作只能在一端进行，他按照先进后出的原则存储数据。

    image-20241210091132541

  4. 队列

    ​ 优先队列的区别是队列元素被赋予了优先级，插入元素未必直接插入队尾，而是按照优先级进行存取，删除元素时也是优先级最高的元素被删除。

    ​ image-20241210091144620

二、搜索算法

  1. 搜索算法–DFS

    DFS算法常用于对树或者图进行遍历。深度优先搜索会尽可能深得搜索树或者图的分支直到树或者图的所有节点均被访问。

  2. 搜索算法–BFS

    BFS算法常用于对树或者图进行遍历。广度优先搜索会尽可能宽得搜索树或者图的分支直到树或者图的所有节点均被访问。

    ​

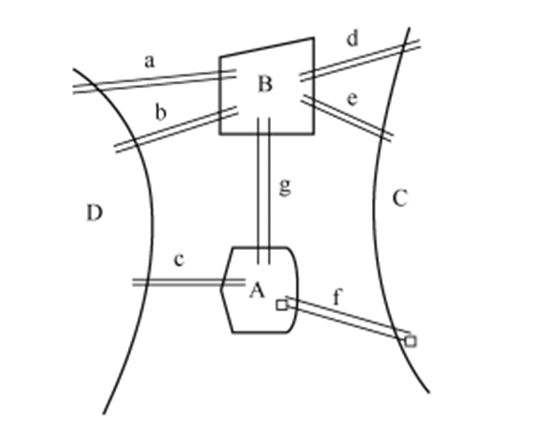
三、七桥问题

​ 河上有两个小岛，有七座桥把两个岛以及河岸联系起来，一个步行者如何不重复的，不遗漏的一次走完所有桥并且最终回到出发点。

image-20241210091340866

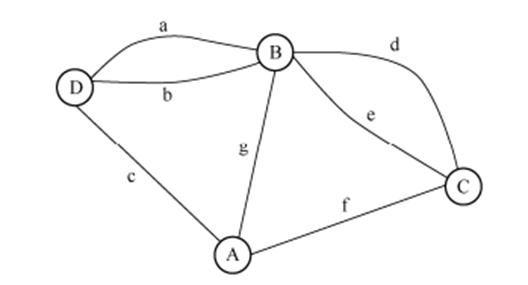
七桥问题解法

首先我们将七桥问题转换为一个图问题。

image-20241210091404810

代码实现如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
#七桥问题:
vertex = ['A', 'B', 'C', 'D']
v2edge = [['c','f','g'],['a','b','d','e','g'],['d','e','f'],['a','b','c']]
v2v = [[3,2,1],[3,3,2,2,0],[1,1,0],[1,1,0]]

def dfs_bridge(vs,edg_num,v_path,edge_path):
    v_top = v_path[-1]
    if v_top == vs and edg_num == len(edge_path):
        print("起点是：",vertex[vs])
        print("依次通过的桥为：",edge_path)
    out_degree = len(v2edge[v_top])
    for i in range(out_degree):
        if v2edge[v_top][i] in edge_path:
            continue
        v_path.append(v2v[v_top][i])
        edge_path.append(v2edge[v_top][i])
        dfs_bridge(vs,edg_num,v_path,edge_path)
        v_path.pop()
        edge_path.pop()
for i in range(len(vertex)):
    dfs_bridge(vs=i,edg_num=7,v_path=[i],edge_path=[])

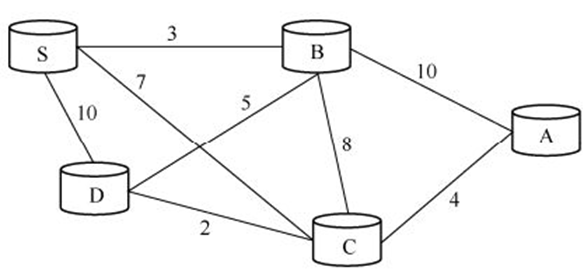
四、旅行商问题

​ 选择一条旅行路径，该路径的限制是每个城市只能去一次并且不能漏掉某个城市，最后回到原点。

image-20241210091745259

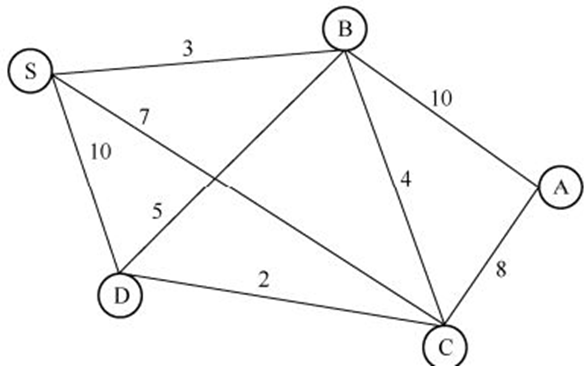
七桥问题解法

将城市看作顶点，将城市之间的路径看成边。

image-20241210091824917

代码实现如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
#旅行社问题：
vertex = ['A','B','C','D','S']
v2edge = [[10,8],[10,4,5,3],[8,4,2,7],[5,2,10],[3,7,10]]
v2v = [[1,2],[0,2,3,4],[0,1,3,4],[1,2,4],[1,2,3]]
def dfs_TSP(vs,v_num,v_path,dis,min_dis):
    v_top = v_path[-1]
    out_degree = len(v2edge[v_top])
    for i in range(out_degree):
        vs_i = v2v[v_top][i]
        if vs_i == vs:
            if v_num == len(v_path) and dis + v2edge[v_top][i] < min_dis[0]:
                min_dis[0] = dis + v2edge[v_top][i]
                new_path = []
                for item in v_path:
                    new_path.append(vertex[item])
                new_path.append(vertex[vs_i])
                print("new distance:",min_dis[0],"new path:",new_path)
            continue
        if vs_i in v_path:
            continue
        v_path.append(v2v[v_top][i])
        dfs_TSP(vs,v_num,v_path,dis + v2edge[v_top][i],min_dis)
        v_path.pop()
min_dis = [10000]
for i in range(len(vertex)):
    dfs_TSP(vs=i,v_num=5,v_path=[i],dis=0,min_dis=min_dis)

五、实验结论

穷举搜索法的优点

  • 直观易懂：穷举搜索法通常基于问题的直接描述，易于理解和实现。
  • 正确性保证：由于穷举搜索法会检查所有可能的解，因此它能够确保找到问题的最优解（如果存在的话）。
  • 适用性广泛：这种方法适用于许多问题，特别是那些没有更简单或更有效算法可用的问题。

穷举搜索法的缺点

  • 计算量大：穷举搜索法需要检查所有可能的解，因此计算量通常很大，尤其是在问题规模较大时。
  • 效率低下：由于需要检查大量解，穷举搜索法通常非常耗时，可能在现实应用中不可行。
  • 资源消耗多：在处理大规模问题时，穷举搜索法可能需要大量的内存和计算资源。

使用穷举搜索法需要注意的问题

  • 问题规模：在使用穷举搜索法之前，需要仔细评估问题的规模。如果问题规模太大，穷举搜索法可能不是一个好选择。
  • 优化技巧：尽管穷举搜索法本身可能效率低下，但可以通过一些优化技巧（如剪枝、排序、哈希等）来减少计算量和提高效率。
  • 利用问题特性：在某些情况下，可以利用问题的特性（如对称性、单调性等）来减少搜索空间或优化搜索过程。